Part 33: Three Houses

Pandora's Box (Live Version)
hey so this is cool and good please listen to it!!





3. The time difference has the reverse effect of the flight returning to Los Angeles. If the plane to Los Angeles left New York at noon New York time, you could also say it left New York at 9 a.m. Los Angeles time.

Despite the premise, this is still a pretty simple math puzzle, all told.










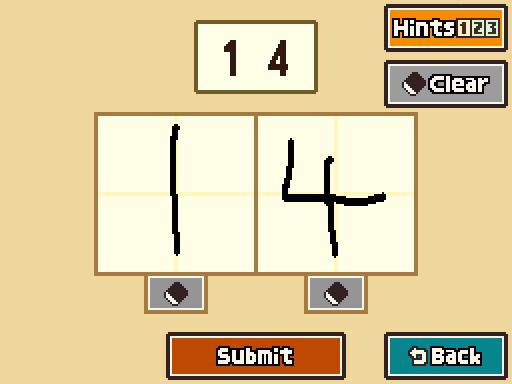
3. Chunk D forms a part of the front-left side of the large cube. Use that information to start reconstructing the structure in your head. As the pieces come together, the answer should become clear.

Normally I kind of have trouble mentally picturing how these fit together but in this case it's pretty easy even for me. I think that they're fixed in this orientation helps a lot, though.






Puzzle 141 Disappearing Act 6





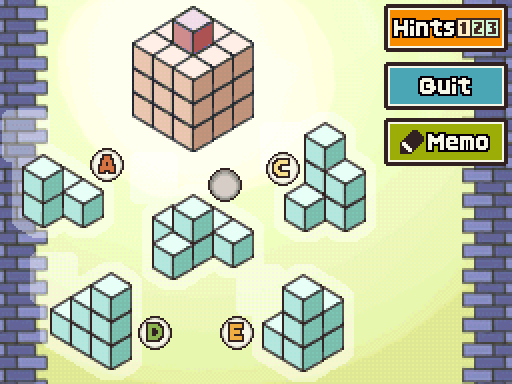
1. You have quite a few balls to get rid of, so you'll have to do a lot of jumping. Just make sure you aren't choosing your moves at random, or you'll end up getting stuck before you finish. Plan out your jumps so that you never leave any balls out away from the group where you won't be able to reach them later.
2. As you reduce the number of balls on the board, those remaining take on a configuration that you've previously solved. If you made it this far, this puzzle is in the bag for you.
3. Sorry, there are no more hints to be had for this puzzle. You may have heard that proper peg solitaire players don't consider these puzzles complete unless the remaining ball ends up in the center space. One step at a time, though. Let's finish this puzzle first.

Okay, so this is the closest thing there is to a proper standard Peg Solitaire puzzle at long last. Still don't have to end in the middle but the easiest solution makes that available anyway so why wouldn't you?




End





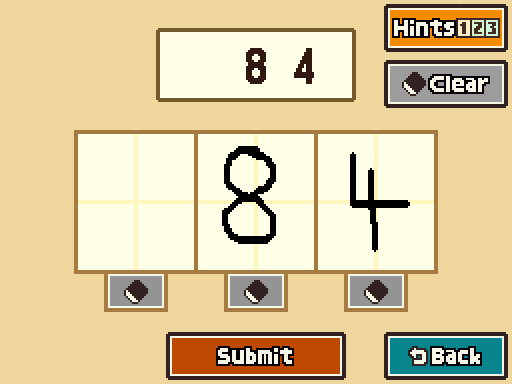
3. The lowest common denominator of 2, 6, 7, and 12 seems to be the same as the length of the mathematician's life expressed in years.

As written, this puzzle was very convoluted and confusing but when you cut the chaff it becomes easier to understand.










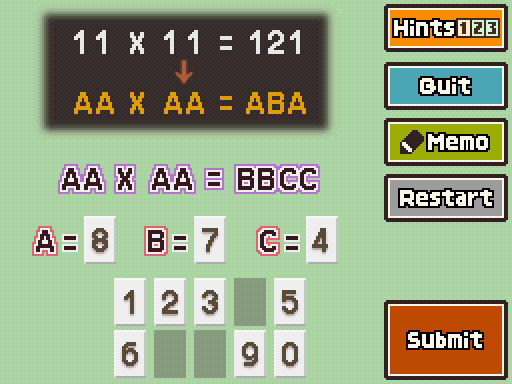
3. As detailed in Hint Two, if you substitute every digit for A and work your way up, you'll find the answer in the last half of your search.

This one is honestly kinda hard to figure out simply, but very easy to figure out quickly. Just hammer combinations in a calculator until the number you square results in a BBCC answer.






Puzzle 144 Super Pancakes





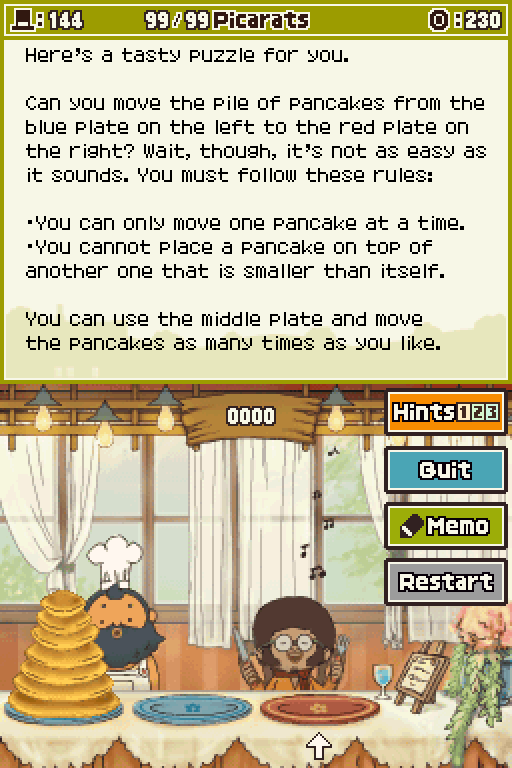
1. The method for solving pancake puzzle has been described in many other hints. Move the smallest pancake over to the middle plate, then move the next-smallest cake to the right plate. Then stack the smallest cake on top of the one right. Next, take a new, slightly larger pancake from the stack on the left and move it onto the open middle plate. Read more on what to do next in Hint Two.
2. From where Hint One left off, put the smallest pancake on the pancake sitting on the middle plate. Then move the pancake on the right plate over to the stack on the left. Bring the smallest pancake you have over to sit on top of the stack of pancakes on the left plate. You can solve this puzzle by repeating the process outlined in Hints One and Two while introducing bigger and bigger pancakes, but it's not very efficient.
3. Aim to limit the number of moves you make to keep yourself from getting confused along the way.

Being just another Tower of Hanoi puzzle, this isn't particularly difficult or anything. But the thing about Towers of Hanoi is that they get really long, really fast. Based on optimal solutions, this one is by far the longest puzzle yet.

...Based on (my) average solutions, it pales in comparison to most sliding puzzles.








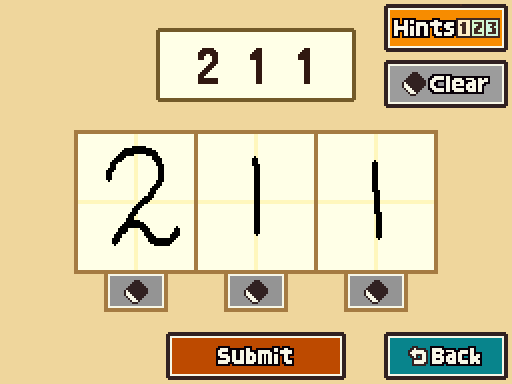
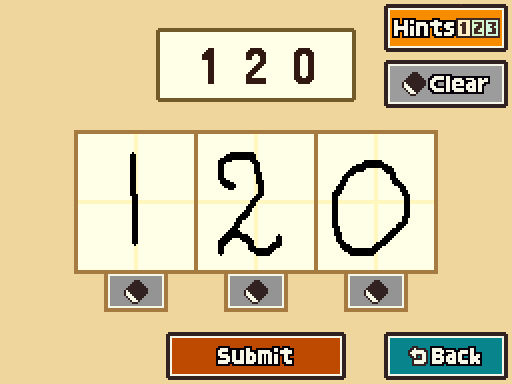
3. The number the magician was after is greater than 400, but the number of pearls the adventurer brought back was actually in the range of 200 to 300 pearls. Remember, you're out to find the number of pearls the adventurer decided to bring back.

Adventurer failed his quest because he failed his maths classes.






It's really not hard to get 421 as the intended solution! 211 is obviously wrong, because that gives 3 left over when divided by four. 212 is so obviously a multiple of 4 that it's astounding!





3. Think about the regular geometric figures you can create with points A, B and C. You could create a regular hexagon, couldn't you? And the internal angles of regular hexagons are always 120 degrees.

Mentioned it before, but the lack of any numbers make this easier than it would be otherwise, since it helps remove the risk of overcomplication. This is a real risk of happening with all math puzzles, as has been witnessed countless times in the past.






Also wow I just noticed but Hint 3 outright tells you the answer. Not even in a coy wink-wink, nudge-nudge way. It just spells it straight out. You'd think I'd have noticed it before but I hadn't looked at it before so...

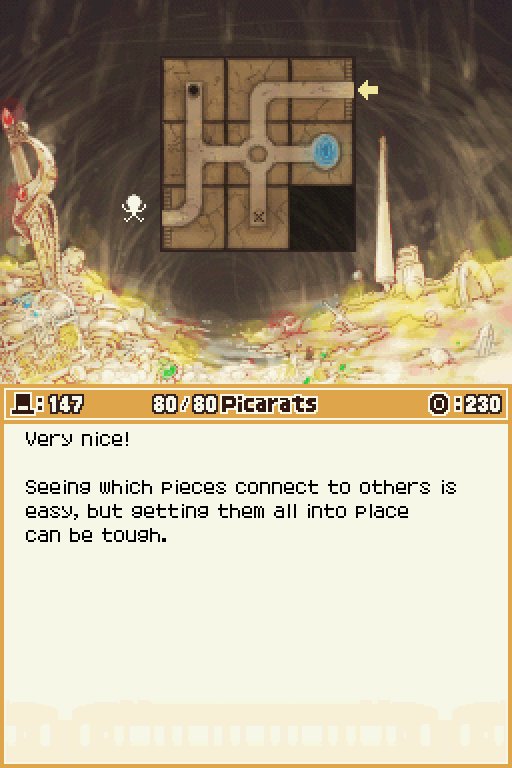
Puzzle 147 Sliding Labyrinth





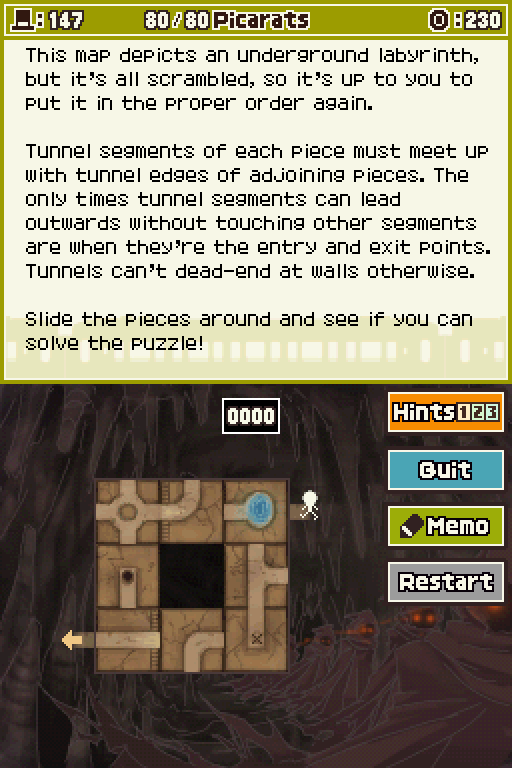
1. Just moving pieces around randomly probably won't help much. Think about the position of pieces on the grid as dictated by where their tunnel segments are placed.
2. The piece connected to START! is the straight horizontal tunnel. Leave the bottom right square on the map open.
3. The pool is below the start section. The cross-shaped tunnel goes in the center of the map.

Honestly, for an intended to be hard sliding puzzle this one is... really easy. It should not at all be worth 80 Picarats because it's far easier than a lot of earlier ones!






So, next up on the list is the first actually real postgame set of puzzles.



And unlike before, all 3 of these CAN be done in-thread!





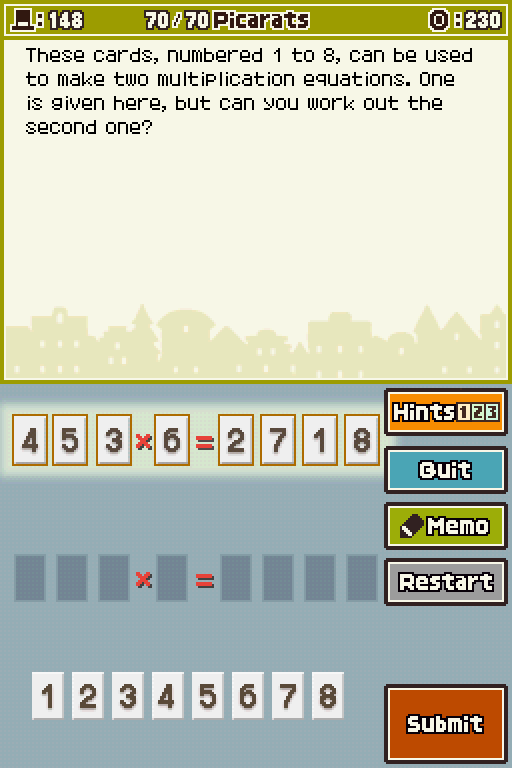
1. The product has four digits, the first of which is one.





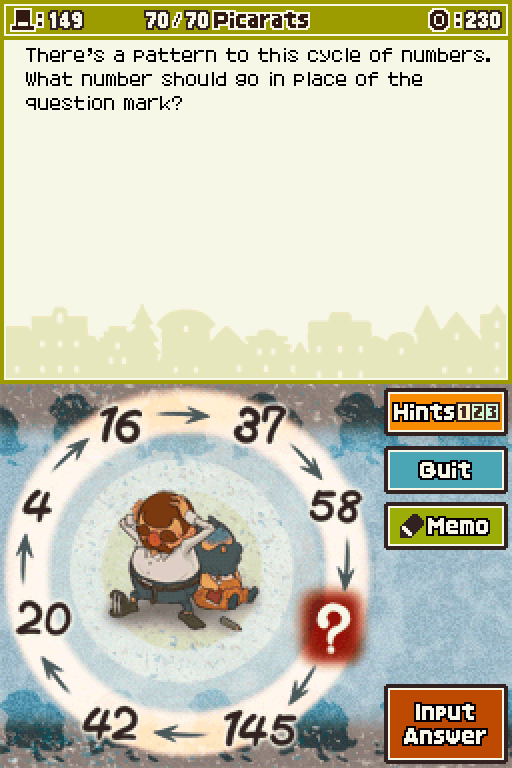
1. Try treating each digit of a number as a separate entity.
2. Try to find a rule that uses the digits from one number to create the next number in the cycle.





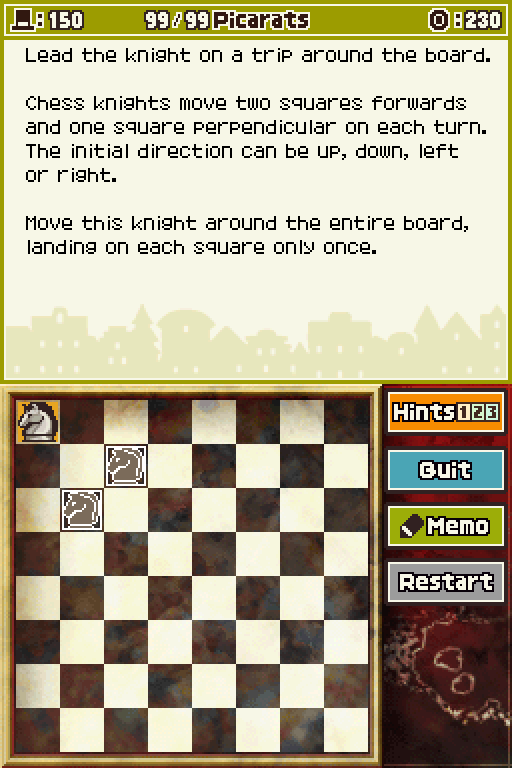
1. This board is eight spaces by eight spaces, just like a regular chessboard. That means this puzzle is just like the original knight's tour. There are no hints to be had here! Just work it out on your own.


Yeah, so I did all the main-game versions of this without thread input and now you get to handle the hardest one on your own!

...In part because it's doable like that and in part because I'm sure someone probably wants to anyway.



For the sake of having more puzzles, let's pretend that those 3 have been solved now and that brings our total up to 150. That lets us access the last set of 3.



Curious Village made these worth relatively low amounts for when they came.



Thankfully, that's not the case here.



1. This is a hard puzzle, so maybe this hint will help. The first thing you need to do is create an answer key based on the three scored tests. Since Mary got the highest score, try creating a key that compares her answers to everyone else's.
2. The three graded tests agree on four questions. However, you know that not all four of these are correct because Lisa only got a score of 30. You also know that not all of these "agreed" answers are incorrect because Mary had a score of 70.



So this set of three aren't all worth 99 (even though that'd be sensible for the placement!) but whatever. It doesn't matter; by now we have more than enough Picarats for everything they're used for anyway.



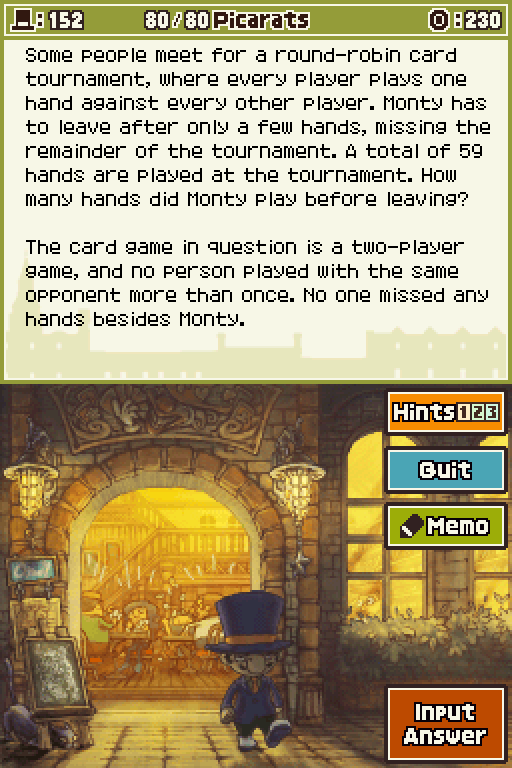
1. Mock up an equation with the number of people and the number of matches played as variables. That would be a good place to start.
2. In order to create the equation for the number of hands, you would need to multiply the number of players by the number of players minus one, then divide this product by two. If there were three people, there would have been three hands. If there were four people, there would have been six hands. You can assume from the conditions given that if no one left, the minimum number of hands would still have to be at least 60.

Of course, 153 is a sliding puzzle. The last puzzle of (almost) every set here has been one so it makes sense, but also Curious Village's final puzzle was a sliding puzzle too. I can't really complain about it being consistent I guess.