Part 53: 5-8

Okay, so let me take this opportunity to remind those of you who already know what's going to happen to not post any spoilers at all. Not even sarcastic wink-wink-nudge-nudge stuff. We've got a billion questions that are finally going to get some answers, so if you actually know what they are hold off on posting about them until they happen.

That out of the way, let's finally get started on our fourth attempt at this thing.

[Video: Introduction]
Oh, right, you can watch this now. Everything in it that's an explicit spoiler has been seen at some point now.



...Well, actually before we continue any further I'm going to explain very briefly how endings have worked so far and what makes this next path actually different.

As you might have guessed already, the endings we do get are determined by the doors we pick... to a point. The only door that matters - usually - is the last door. Door 1 gives us the Axe Ending, Door 2 gives us the Submarine Ending and Door 6 gives us the Knife Ending. Door 3 railroaded us through Door 2 automatically, for example, so that's essentially one and the same.

This time, though? We need to pick doors in a very specific order. This order makes a lot of sense, since we are following an actual plot thread as we go along. However, there is no indication that this thread is even there; unless you are actively following it... it doesn't exist. There's one real hint we've seen that we missed something before and that was a "scene" in one room that lasted for about 20 seconds.

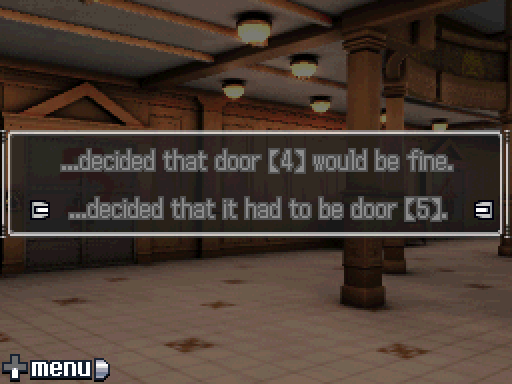
So, our first door is Door 5.

[Music: Binary Game]



The actual cabin itself is, sadly enough, not particularly interesting.



The most interesting thing is this thing on the table. We didn't look at it before, because there was no point to it. So, because I know at least one person wants it, we might as well do so now.



It looks like you could slip something into it, but there's nothin' in there.



So you think this was for filing sports scores or something?
No, I don't think so... I think "SCORE" probably means musical score.
So this is like a folder for some sheet music or something.

And that's all there is to this thing. Ayup. Nothing particularly exciting, sorry.

That amounts to a lot of the room, really. All there is in here is learning about Seven's amnesia, finding a map that somehow isn't in the 2nd Class Cabin if we come through here, and a scene with Snake.

...Since that last one is actually vaguely important for things we'll see behind the next door on our itinerary, though, I'd consider this scene worthwhile enough to repost in full since it's been a loooong time since we last saw it.



Blind or not, Snake was clearly attempting to do something.

At last, Junpei could no longer contain his curiosity.

What're you doing?

Snake waited a moment before answering.

I heard something...strange.
...Something strange?
Ah well. Nevermind. It doesn't seem to be anything suspicious. I don't wish to toot my own horn, but my auditory senses are considerably more advanced than those of most humans. I notice even the slightest of noises.
Right, are you gonna tell me you can hear a needle drop from a mile away?



However, by listening to the sound of footsteps and breathing as well as sound echoing off the environment, I can locate most objects.
Oh yeah, that's right.
When Clover fell on the big staircase a little while ago, you were at her side immediately. So that was...hm.
Yes. I could hear it happening. In fact, I can run quite fast--certainly as fast as you. And should someone attempt to start a



Junpei was somewhat taken aback by this revelation. He stared at Snake, skeptical.

You don't believe me, do you? Care to give me a try? I must warn you, you'll no doubt regret it.
...



Other than that, there's nothing else of interest in here so we'll leave...



Seven will jam the door open...



We'll go through the entire casino without anything of interest or worth noting happening.

Then we go to the large hospital room, meet up with everyone else, blah blah blah you know the routine here.

[Music: Extreme Extrication]



Santa remains the only person of importance when looking for Snake, and we only have Lotus left to accuse.



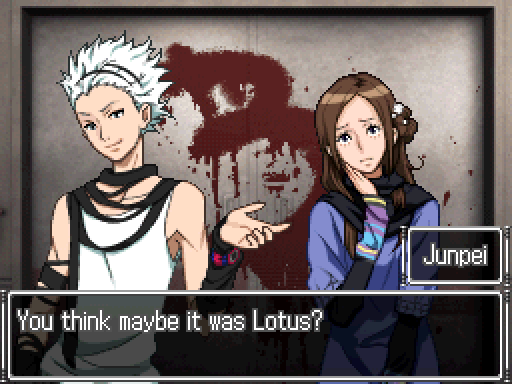
They say the 1st person at the scene is the most suspicious...
Hm... Yeah, that's possible. You don't have anything else to suggest she did it, though. You might as well just suspect everybody.

Junpei furrowed his brow.



And with that, we're done here.



Our second door is going to be Door 8. Again, we must choose Door 8 here.

We're not really interested in the room itself, so we'll just skip over that.



We are, however, interested in this computer once we can fix it up. We'll give it power, and then Lotus can do her thing again. Though because we went through door 5 last time, this scene has now changed greatly for no reason whatsoever.

[Music: Silence]



With a soft hum, it turned on...



Huh...? It's actually working?
So it would seem.
Uh... Isn't that kinda...weird?
What?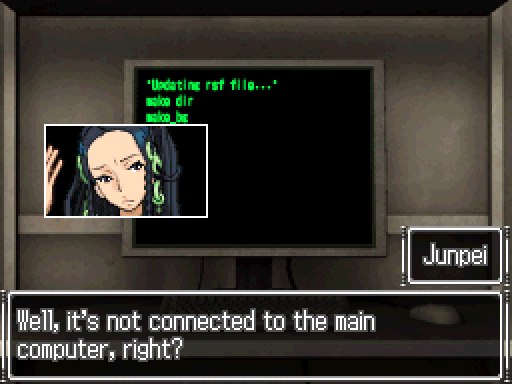



There's just this keyboard and monitor. The only cable connected to this thing is the power cable we just plugged in.
So...why is it working?



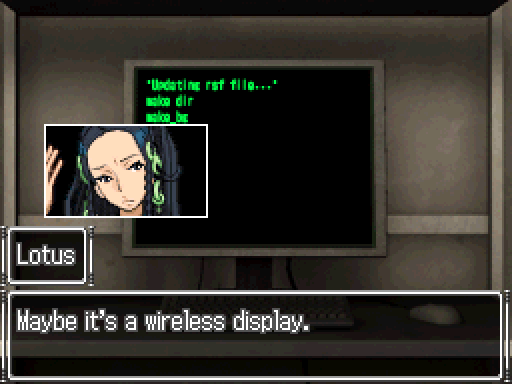
Clearly, this was a reasonable explanation to Lotus.

A...wireless display?
Yes, it connects to your computer wirelessly. Hence the name. Have you been living in a cave, Junpei?

He most certainly had not, but...

Is that...normal...?



?

As they spoke, the lines of letters suddenly stopped, and disappeared.

The only thing left on the screen was the word "pass", followed by a colon.



Again. There must be a hint around here somewhere...
Could you go take a look?
Yeah. I'm on it. What are you going to do?



On your own?
Yup, on my own.

Lotus pulled over the nearest chair and dropped herself down onto it, in front of the keyboard.



All right, let's kick some ass.

Lotus smiled to herself and rubbed her hands together in anticipation.



Uh... Wh-What?!

Junpei was, for once, at a loss for words.

Didn't expect that, did you?
Of course I didn't! What kind of job do you have?! What are you!?
I'm unemployed at the moment.



Why?

Lotus blinked.

Huh? Oh...um... It was just...something.



Lotus's fingers began to move again, and in a few seconds she was back up to speed.

As she typed, more letters and symbols that meant nothing to Junpei began to pour across the screen.

Uh... What are you doing now?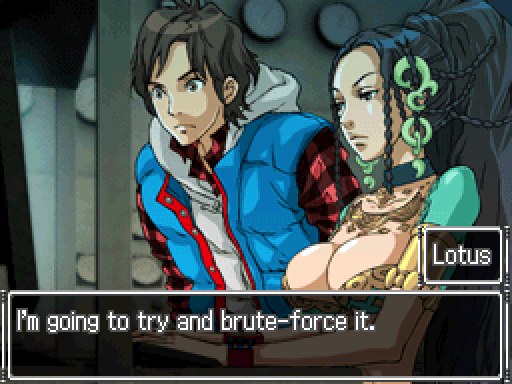



Brute...what?
A brute force attack is... Well, the short version is that I just attack the thing head-on. The long version...

Without looking up, or slowing down, she began to explain.



It's not the most elegant solution, certainly... But, given the circumstances, there isn't much else I can do.

Even as she talked, her fingers never slowed or missed a key.

Junpei couldn't help but feel a little awed.

Oh, but back to what we were talking about earlier...
What were we talking about?



It's kind of strange if you think about it, isn't it?
?
Hmm... How do I put it...

[Music: Riddle and Puzzle]

Well, let's say you write a program that calculates an addition problem for you, all right? So you enter 1 + 1. The screen will show you 2. See? Isn't that strange?
U-Uh...no? Not really...



You said so just a minute ago.
?
You're just not getting it, are you? Who calculated 1 + 1?
The...uh, the main computer, right? You said it's connected to the monitor wirelessly.
Yeah, but someone who grew up in a cave wouldn't know that, right?



And once they've decided that, they'll start examining this monitor. They might poke the screen or something...
"Ah, I see, the color changes when I press it here..."
Then they might investigate the hardware on the inside...
"Ah, I see, so this wire supplies power..."
Eventually, they might even cut the wires...
"Ah yes, just as I expected. When this wire is cut, no results appear...Therefore, it must be this device which does the calculations!"
...



But these cave people wouldn't know that. Because they have no idea that the monitor and the computer are connected wirelessly.

Lotus continued to type.

Junpei scratched his head.



Nothing. Really. It's just... I thought maybe...



...Huh?
Well, let's say you stick a bunch of electrodes into parts of the brain. A scientist examining the signals they send out might say... "Interesting, so stimulating this part of the the brain causes this person to see colors... That must mean this neuron cluster controls that function. Okay, let's see what happens when I cut out this part... Ah, just what I thought! Cutting off this part causes that function to cease! Therefore, human thought processes must occur in the human brain!" You get it? It's just like this monitor.
...
Maybe the brain is just an output device--like this monitor.



...We just don't know it. We never even think about it. Just like those cave people wouldn't know about wireless communications. We can't imagine that there's some unknown medium that transfers information into our brains, where we experience that information as thoughts.

Junpei didn't say anything.

Not so much because he had no retort. No, her argument just seemed...silly, and he was a little surprised to be hearing something like it from someone like her.



It sounds kind of similar to solipsism. I say "kind of" since it's not really the same thing, but it's more or less the general idea. At least, it is as far as I understand it.



Oblivious to Junpei's increasing discomfort, Lotus continued.

If memory is actually stored somewhere else, in some sort of "main body" somewhere... Maybe he hasn't "forgotten" anything at all.
He's just having a difficult time accessing his memories because the monitor--his brain--has been damaged.
...
I suppose that would explain aphasias and blindsight, too. Perhaps they actually can speak, or see... The monitor just isn't functioning properly.



W-Wait a minute... Pro...sop-what?

He knew what aphasia was from watching medical dramas on TV, and blindsight was easy enough to guess, but he'd never heard the word "prosopagnosia" before...

What, you've never heard of prosopagnosia?

Lotus spun around in her chair to look at him.

Junpei just shrugged and shook his head.

Nope. What is it?
Well, put simply, it means a condition where



In other words, my face would look the same as Clover's, or even yours. So they can't remember faces, which is how most people recognize each other. That means that people with prosopagnosia have trouble recognizing even people they're close to. Usually, they can make do by associating



Does that mean other people's faces look...like...blanks?
No... No, I don't think so. You've seen monkeys, like in a zoo, right?



Even though they've obviously got faces it's almost impossible for a human to distinguish between them. The zoo staff that works with them would learn to identify different monkeys eventually, but you or I couldn't, unless one had a scar or something else to set it apart.



Prosopagnosia, huh... Didn't even know that kinda thing existed...

Junpei did his best to act as though the entire lecture hadn't gone entirely over his head.

And...uh...what were we talking about?
The idea that your brain is just an output device, like a monitor.
Are you serious about that stuff?



What about the other half?
Well...



...
...
Not funny...



[Music: Silence]

It's nothing more than a story I made up out of boredom. Don't take it seriously.
It was the first thing that came to mind, and I just talked about it to kill time.



...Why?
I don't have to kill time any longer.

As she spoke, Lotus raised her right arm high...

And brought it down on the Enter key.



*Giggle* Piece of cake.

Lotus would clearly have patted herself on the back, if it would not have made her look entirely ridiculous.

After a few seconds, the "Accepted" disappeared, to be replaced with...



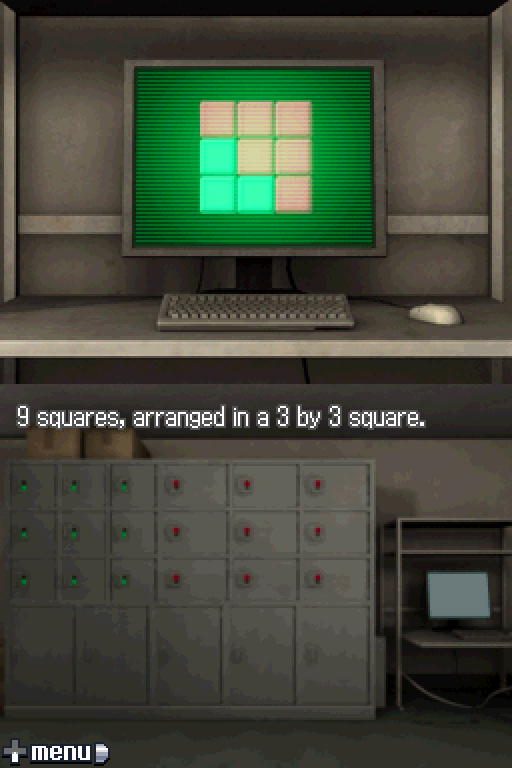
What the hell is that...
No idea. It looks like a puzzle.

Suddenly, Lotus stood up.

...Huh? Aren't you gonna...I dunno...do more computer stuff?



See, the keyboard... Nothing. So, there's nothing more I can do.
Umm...
Well, I guess I'll leave this to you then, Junpei.
What!?
Let me take a break, all right? I did my part.



Junpei crossed his arms and stared at the puzzle shown on the screen.

[Music: Quaternary Game]



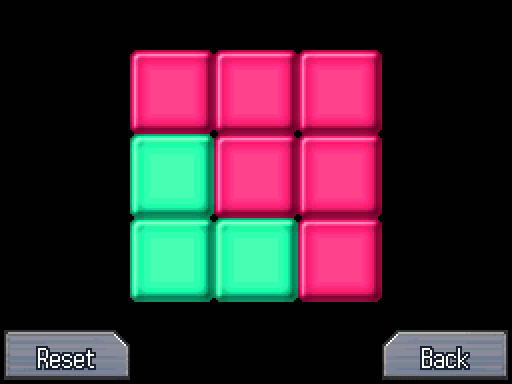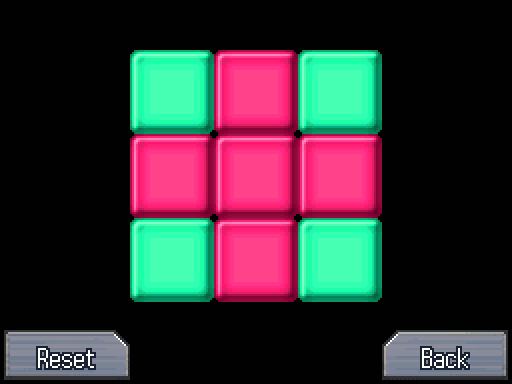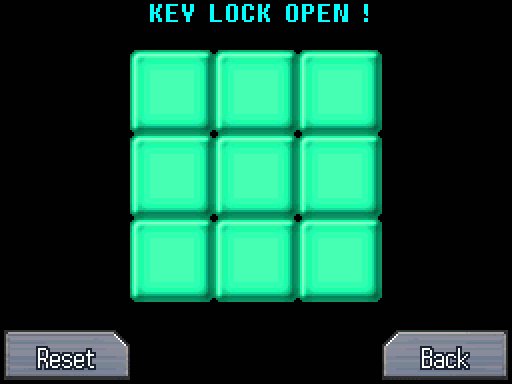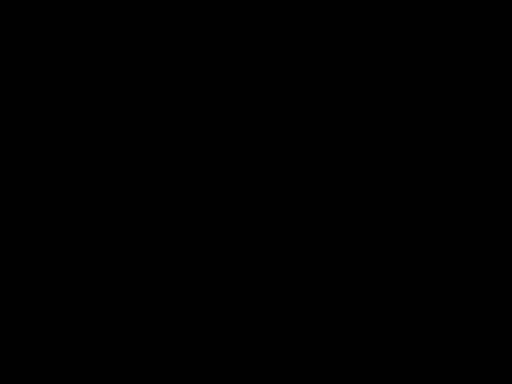
We need to solve this before we can do anything else. Afterwards, the locker opens up and we can get the activation key to start a fire. Oh and the Earth Key too.

That brings us straight too...



Hey Junpei, do you have a minute?

He put the puzzle aside for the moment, and walked over to Clover.

What's up...?

[Music: Silence]



...?



In fact, by doing so we turned this bit into a proper cutscene rather than the like 5 lines it was before.

Did you hear him say, like...anything weird?

Why is she asking me this, Junpei wondered.

The more he thought about it, however, the more it made sense. Snake had been gone for a long time.

Clover was quite attached to her brother. Of course she would have been worried about him.

[Music: Imaginary]

He thought back to when he'd gone through door [5], hoping he might remember something, even a small something, that would help her.

However...



I mean, he did mention that his hearing "exceeds that of a regular person", or something like that, but... That's about it.
Okay...

Clover's words were barely audible. She nodded vaguely to Junpei, and turned to walk away.

Uh, hey, wait a minute...
...Hm?
Look, I don't know if I should...ask you things, but... If you don't mind, I was hoping you could tell me if...uh...



You're talking about his eyes?
Yeah...
No... He wasn't born blind.



A really bad car accident. He couldn't see after that... And...his arm...
...His arm?
Yeah... My brother's left arm is...um, it's not like a normal person's arm...



The accident hurt him really bad... To save him, they... They had to cut off his arm...
...
...
...
Is that all you wanted to ask me?

Talking about her brother had clearly taken a great deal out of Clover. Junpei nodded.



From here, there's nothing much new we need to worry about. We finish this room in a way that I'm still not convinced is how we're meant to do it, get the keys we're missing from Seven and Lotus, split up to check out various areas then reconvene at the large hospital room again. At this point, we learn that Snake's dead and go check out his body because that sounds like a good idea.

After that, we discuss the possible MO of Snake's death, whether Zero's around on the boat, and if so maybe he's one of us. We get nowhere with those topics, other than a couple of possible ideas and then we head back to pick our final door for this path.



Really, this last choice is... kinda dickish, actually. Unlike with going to 8 after 5, there is a hint as to which is "right" and which two are "wrong"... but it's very minor, easily forgettable and even if you know what it is, it still doesn't stand out. You might remember it, you might not.









An alternative design for Lotus both with and without jacket.